高考数学(理科)小题狂做·基础篇
P89 Q6
不论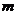 取何值,直线
取何值,直线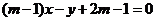 都过定点 ( )
都过定点 ( )
A.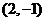
B.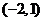
C.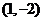
D.
考点说明:直线的方程
问题解答:显然所求定点与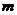 无关,故将直线方程按
无关,故将直线方程按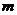 进行分类,含
进行分类,含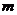 的项与不含
的项与不含 的项分类后,令
的项分类后,令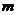 的系数为0,再令不含
的系数为0,再令不含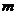 的项为0,解方程即可。
的项为0,解方程即可。
Q8
已知点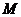 是直线
是直线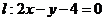 与
与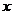 轴的交点,将直线
轴的交点,将直线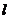 绕点
绕点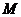 逆时针旋转
逆时针旋转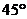 ,得到的直线方程是 ( )
,得到的直线方程是 ( )
A.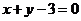
B.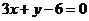
C.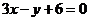
D.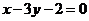
考点说明:直线的方程
问题解答:本题的重点是求出旋转后的直线的方程,可先求出点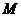 的坐标,之后根据两条直线倾斜角的关系求斜率,即
的坐标,之后根据两条直线倾斜角的关系求斜率,即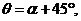 两边取正切即可。
两边取正切即可。
Q9
若直线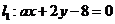 与直线
与直线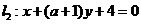 平行,则实数
平行,则实数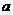 的值为( )
的值为( )
A.1
B.1或2
C.-2
D.1或-2
考点说明:直线的平行
问题解答:对于用一般式写出的直线方程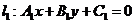 与
与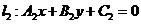 ,若两直线平行,则其充要条件为:
,若两直线平行,则其充要条件为: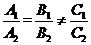 ,由此结论可得答案。
,由此结论可得答案。
Q10
若直线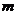 被两平行线
被两平行线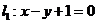 与
与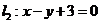 所截得的线段的长为
所截得的线段的长为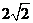 ,则
,则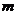 的倾斜角可能是 ( )
的倾斜角可能是 ( )
A.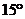
B.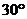
C.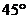
D.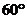
考点说明:直线的倾斜角;平行线间的距离
问题解答:如图
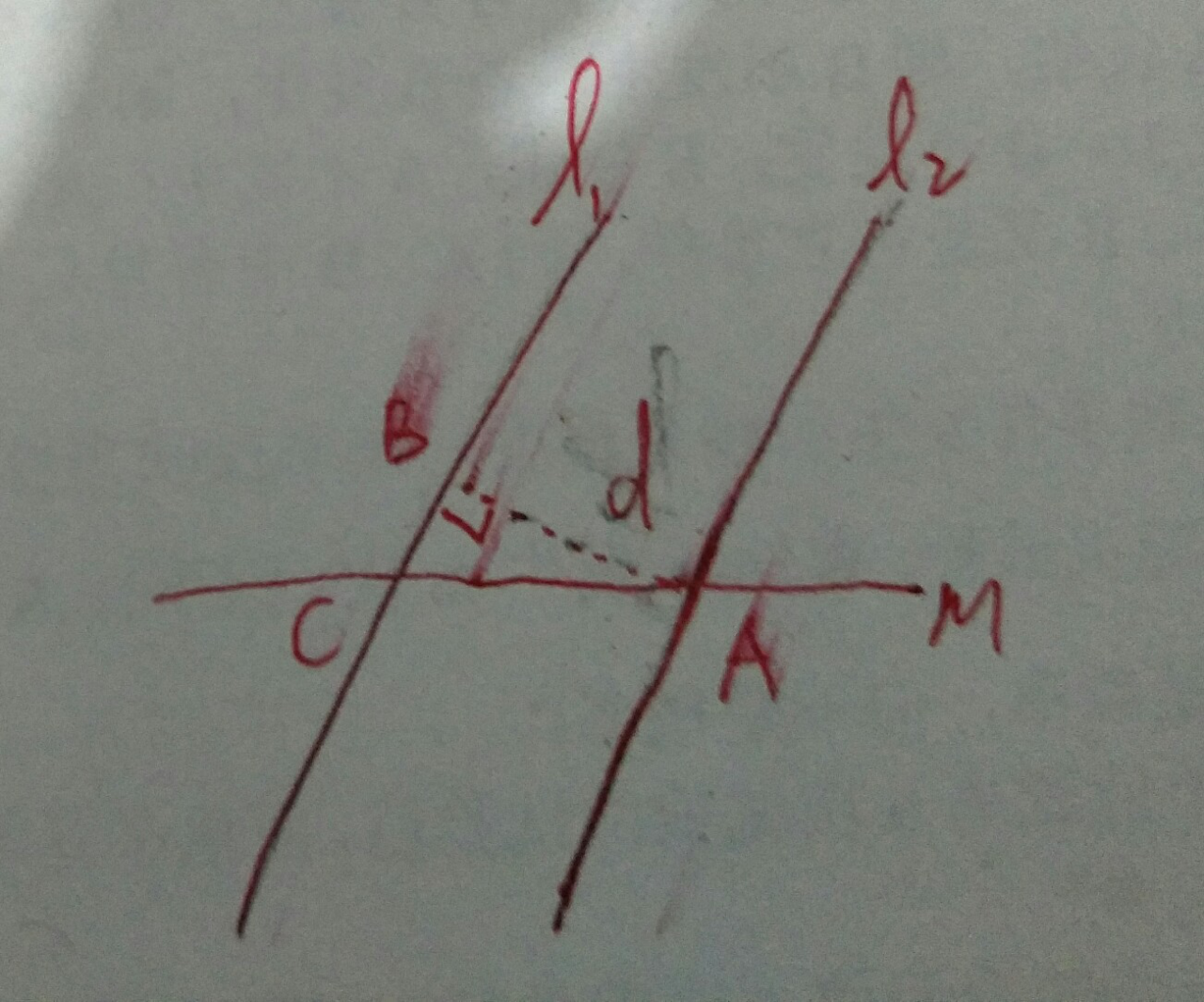
易知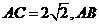 为平行线间的距离,在直角三角形
为平行线间的距离,在直角三角形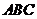 中,易求得
中,易求得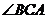 (或
(或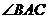 的大小),再根据平行线的倾斜角便可求得所求直线的倾斜角。
的大小),再根据平行线的倾斜角便可求得所求直线的倾斜角。
P90 Q11
两平行直线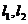 分别过点
分别过点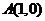 与
与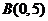 ,则
,则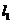 与
与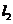 的最大距离为 ( )
的最大距离为 ( )
A.3
B.4
C.5
D.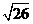
考点说明:平行直线间的距离
问题解答:若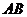 与平行线垂直,则两平行线间距离最大,建议可以通过固定两点对平行直线进行旋转来体会上述结论。
与平行线垂直,则两平行线间距离最大,建议可以通过固定两点对平行直线进行旋转来体会上述结论。
Q12
(新课标II真题)已知点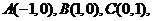 直线
直线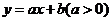 将△
将△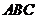 分割成面积相等的两部分,则实数
分割成面积相等的两部分,则实数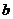 的取值范围是 ( )
的取值范围是 ( )
A.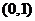
B.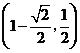
C.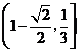
D.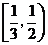
考点说明:直线的方程
问题解答:本题解法较为传统,如图: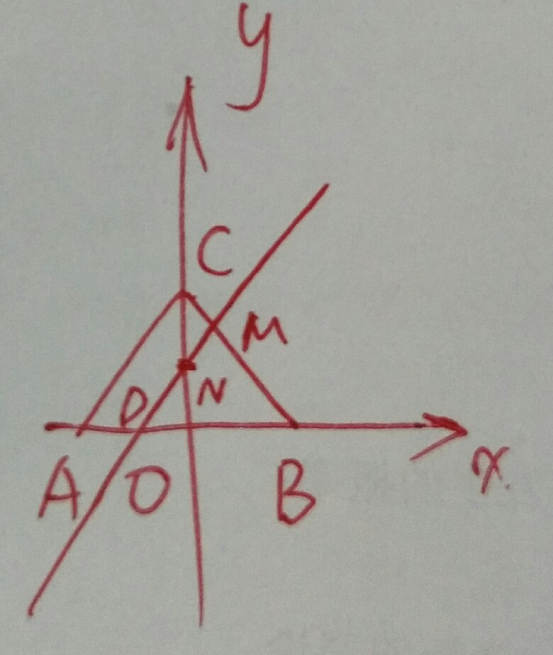
根据已知条件可知△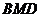 的面积即为△
的面积即为△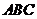 面积的一半,可通过求出
面积的一半,可通过求出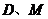 两点的坐标确定△
两点的坐标确定△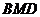 的面积,从而可求得
的面积,从而可求得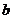 满足的关系式,根据
满足的关系式,根据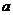 的不同取值可求出其范围;
的不同取值可求出其范围;
要求端点的值时注意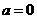 时不可用此方法计算,需单独画图。
时不可用此方法计算,需单独画图。
P97 Q8
已知椭圆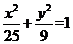 上一点
上一点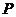 到两焦点
到两焦点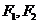 的距离之积为
的距离之积为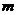 ,则
,则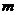 取最大值时,点
取最大值时,点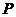 的坐标为 ( )
的坐标为 ( )
A.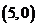 或
或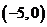
B.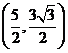 或
或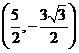
C.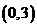 或
或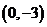
D.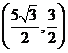 或
或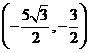
考点说明:椭圆;基本不等式
问题解答:根据椭圆的定义可知 可由基本不等式知当
可由基本不等式知当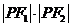 取得最大值时,
取得最大值时,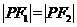 ,从而
,从而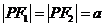 ,可由等腰三角形的性质求出
,可由等腰三角形的性质求出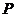 点的坐标
点的坐标
实际上由上述分析易知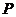 为短轴的一个顶点。
为短轴的一个顶点。
P98 Q9
已知椭圆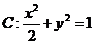 的右焦点为
的右焦点为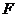 ,右准线为
,右准线为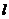 ,点
,点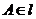 ,线段
,线段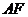 交椭圆
交椭圆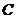 于点
于点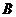 .若向量
.若向量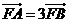 ,则
,则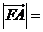 ( )
( )
A.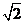
B.2
C.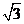
D.3
考点说明:椭圆
问题解答:先由椭圆的准线方程求出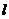 ,而后可根据三角形相似求出
,而后可根据三角形相似求出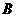 点的横坐标,从而得知
点的横坐标,从而得知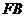 的长,再由条件得
的长,再由条件得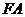 的长。
的长。
Q10
(新课标真题)已知椭圆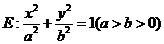 的右焦点为
的右焦点为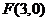 ,过点
,过点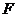 的直线交
的直线交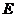 于
于 两点.若
两点.若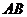 的中点坐标为
的中点坐标为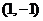 ,则
,则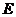 的方程为 ( )
的方程为 ( )
A.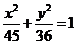
B.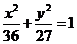
C.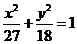
D.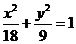
考点说明:椭圆的方程
问题解答:本题使用的方法叫做“点差法”,设出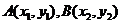 后,带入椭圆方程后两式相减,得到一个关于
后,带入椭圆方程后两式相减,得到一个关于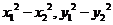 的方程,由中点坐标和直线的斜率可求出
的方程,由中点坐标和直线的斜率可求出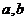 间的关系,再根据
间的关系,再根据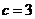 可求得
可求得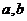 的具体值。
的具体值。
Q12
已知椭圆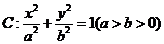 的离心率为
的离心率为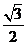 ,过右焦点
,过右焦点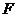 且斜率为
且斜率为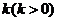 的直线与
的直线与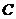 相交于
相交于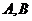 两点.若向量
两点.若向量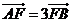 ,则
,则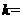 ( )
( )
A.1
B.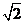
C.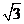
D.2
考点说明:椭圆
问题解答:本题提供的实际条件较少,可用的条件有离心率以及向量的关系,一般可设出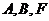 的坐标,然后可根据向量关系得到坐标之间的关系
的坐标,然后可根据向量关系得到坐标之间的关系
设出直线的方程,而后根据数量关系求解即可
求解过程中要注意选好参变量,本题中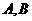 两点的纵坐标的关系较为明确,将直线方程与椭圆方程联立时要注意消去
两点的纵坐标的关系较为明确,将直线方程与椭圆方程联立时要注意消去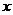 而不是消去
而不是消去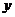 ,甚至在设直线方程时也可以改设成
,甚至在设直线方程时也可以改设成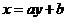 的形式以简化计算。
的形式以简化计算。
P99 Q4
双曲线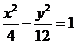 的焦点到渐近线的距离为 ( )
的焦点到渐近线的距离为 ( )
A.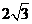
B.2
C.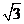
D.1
考点说明:双曲线的性质
问题解答:本题可直接写出焦点坐标及渐近线方程,利用点到直线距离求解
实际上,通过本题可得到结论:双曲线的焦点到渐近线的距离为虚半轴的长。
Q6
(新课标II真题)设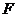 为抛物线
为抛物线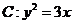 的焦点,过点
的焦点,过点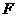 且倾斜角为
且倾斜角为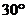 的直线交
的直线交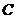 于
于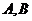 两点,
两点,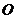 为坐标原点,则△
为坐标原点,则△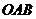 的面积为 ( )
的面积为 ( )
A.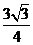
B.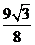
C.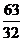
D.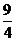
考点说明:抛物线
问题解答:根据抛物线焦点的坐标及倾斜角可写出直线的方程,与抛物线方程联立后有两种做法:
一种是以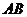 为底,原点到直线的距离为高进行三角形面积的计算,在求
为底,原点到直线的距离为高进行三角形面积的计算,在求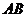 的长时可利用抛物线的性质,本方法较为简便;
的长时可利用抛物线的性质,本方法较为简便;
另一种是利用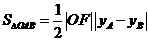 来计算,注意联立时不要消去
来计算,注意联立时不要消去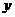 而是要消去
而是要消去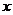 ,利用根与系数的关系进行计算。
,利用根与系数的关系进行计算。
Q7
若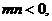 则方程
则方程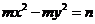 所表示的曲线是 ( )
所表示的曲线是 ( )
A.焦点在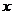 轴上的等轴双曲线
轴上的等轴双曲线
B.圆
C.焦点在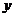 轴上的等轴双曲线
轴上的等轴双曲线
D.等轴双曲线,焦点位置依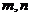 的符号而定
的符号而定
考点说明:双曲线的方程
问题解答:注意将方程化为标准形式,与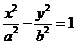 或
或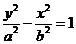 对比后得到答。
对比后得到答。

微信小程序
微信扫一扫体验

微信公众账号
微信扫一扫加关注
评论 返回
顶部

发表评论 取消回复